Question

A rotating wheel requires 2.90-s to rotate through 37.0 revolutions. Its angular speed at the end of the 2.90-s interval is 97.2 rad/s. What is the constant angular acceleration of the wheel?

Answer 1

Angular acceleration,
`\alpha =20.32\ rad/s^2`

Step-by-step explanation:

It is given that,

Displacement of the rotating wheel,
`\theta=37\ rev=232.47\ radian`

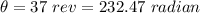
Time taken, t = 2.9 s

Initial speed of the wheel,
`\omega_i=0`

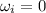
Final speed of the wheel,
`\omega_f=97.2\ rad/s`

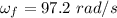
Let
`\alpha` is the angular acceleration of the wheel. Using the third equation of kinematics to find it as :

`\alpha=(\omega_f^2-\omega_i^2)/(2\theta)`

`\alpha=((97.2)^2)/(2* 232.47)`

`\alpha =20.32\ rad/s^2`

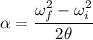
So, the angular acceleration of the wheel is
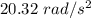`20.32\ rad/s^2`. Hence, this is the required solution.