Answer:
Angular acceleration,
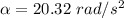
Step-by-step explanation:
It is given that,
Displacement of the rotating wheel,
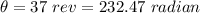
Time taken, t = 2.9 s
Initial speed of the wheel,
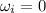
Final speed of the wheel,
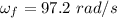
Let
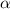 is the angular acceleration of the wheel. Using the third equation of kinematics to find it as :
is the angular acceleration of the wheel. Using the third equation of kinematics to find it as :
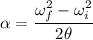
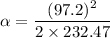
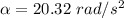
So, the angular acceleration of the wheel is
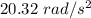 . Hence, this is the required solution.
. Hence, this is the required solution.