Question

As it travels through a crystal, a light wave is described by the function E(x,t)=Acos[(1.57×107)x−(2.93×1015)t]. In this expression, x is measured in meters and t is measured in seconds.

Part A
What is the speed of the light wave?
Express your answer to three significant figures and include appropriate units.

Answer 1

Speed,
`v=1.86* 10^8\ m/s`

Step-by-step explanation:

It is given that,

A light wave is described by the following function as :

`E(x,t)=A\ cos[(1.57* 10^7)x-(2.93* 10^(15))t]`.....(1)

The general equation of wave is given by :

`E=Acos(kx-\omega t)`........(2)

On comparing equation (1) and (2)

`k=(1.57* 10^7)`

`(2\pi)/(\lambda)=(1.57* 10^7)`

`\lambda=(2\pi)/((1.57* 10^7))`

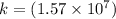
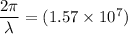
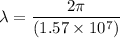
Wavelength,
`\lambda=4.002* 10^(-7)\ m`

`\omega=(2.93* 10^(15))`

`(2\pi)/(T)=(2.93* 10^(15))`

`(1)/(T)=((2.93* 10^(15)))/(2\pi)`

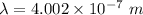
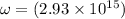
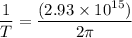
Frequency,
`f=4.66* 10^(14)\ Hz`

Let v is the speed of the light wave. It is given by :

`v=f* \lambda`

`v=4.66* 10^(14)\ Hz* 4.002* 10^(-7)\ m`

`v=1.86* 10^8\ m/s`

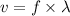
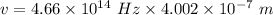
So, the speed of the light wave is
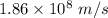`1.86* 10^8\ m/s`. Hence, this is the required solution.