Answer:
1022.485 Watt
Step-by-step explanation:
resistance, R = 12 ohm
Inductive reactance, XL = 15 ohm
Capacitive reactance, Xc = 10 ohm
Vrms = 120 V
Power is given by
P = Vrms x Irms x CosФ
Where, CosФ is called power factor
CosФ = R / Z
Where Z is the impedance
Irms = Vrms / Z
So,
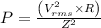
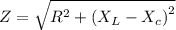
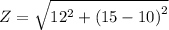
Z = 13 ohm
So,
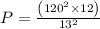
P = 1022.485 W
Thus, the power is 1022.485 Watt.