Question

A rigid tank contains an ideal gas at 40°C that is being stirred by a paddle wheel. The paddle wheel does 240 kJ of work on the ideal gas. It is observed that the temperature of the ideal gas remains constant during this process as a result of heat transfer between the system and the surroundings at 30°C. Determine the entropy change of the ideal gas.

Answer 1

To solve the problem it is necessary to consider the concepts and formulas related to the change of ideal gas entropy.

By definition the entropy change would be defined as

`\Delta S = C_p ln((T_2)/(T_1))-Rln((P_2)/(P_1))`

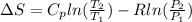
Using the Boyle equation we have

`\Delta S = C_p ln((T_2)/(T_1))-Rln((v_1T_2)/(v_2T_1))`

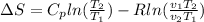
Where,

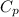`C_p` = Specific heat at constant pressure

`T_1`= Initial temperature of gas

`T_2`= Final temprature of gas

R = Universal gas constant

`v_1`= Initial specific Volume of gas

`v_2`= Final specific volume of gas

According to the statement, it is an isothermal process and the tank is therefore rigid

`T_1 = T_2, v_2=v_1`

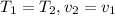
The equation would turn out as

`\Delta S = C_p ln1-ln1`

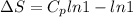
Therefore the entropy change of the ideal gas is 0

Into the surroundings we have that

`\Delta S = (Q)/(T)`

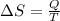
Where,

Q = Heat Exchange

T = Temperature in the surrounding

Replacing with our values we have that

`\Delta S = (230kJ)/((30+273)K)`

`\Delta S = 0.76 kJ/K`

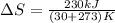
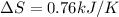
Therefore the increase of entropy into the surroundings is 0.76kJ/K