Answer:
P = 180 watts
Step-by-step explanation:
It is given that,
Inertia of the wheel,
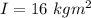
Net torque acting on the wheel,

Initial speed of the wheel,
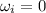
Time, t = 5 s
We know that the relation between the torque and the angular acceleration is given by :
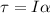
 is the angular acceleration
is the angular acceleration
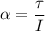

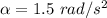
Using first equation of rotational kinematics as :
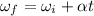
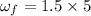
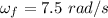
We know that the rate at which the work is done by the torque is called the power of any object. Its formula in rotational motion is given by :
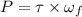
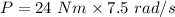
P = 180 watts
So, the power of the wheel is 180 watts. Hence, this is the required solution.