Question

Since the density of air decreases with an increase in temperature, but the bulk modulus B is nearly independent of temperature, how would you expect the speed of sound waves in air to vary with temperature?

Answer 1

To develop this problem it is necessary to apply the concept related to the speed of sound waves in fluids.

By definition we know that the speed would be given by

`v=\sqrt{(\beta)/(\rho)}`

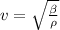
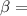`\beta =` Bulk modulus

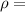`\rho =`Density of air

From the expression shown above we can realize that the speed of sound is inversely proportional to the fluid in which it is found, in this case the air. When the density increases, the speed of sound decreases and vice versa.

According to the statement then, if the density of the air decreases due to an increase in temperature, we can conclude that the speed of sound increases when the temperature increases. They are directly proportional.