Question

(2 points) An article in the Washington Post on March 16, 1993 stated that nearly 45 percent of all Americans have brown eyes. A random sample of n=76n=76 Americans found 28 with brown eyes. We test H0:p=.45 Ha:p≠.45

(a) What is the z-statistic for this test?

(b) What is the P-value of the test?

Answer 1

Answer: a) z=1.43

b) 0.1528

Explanation:

The given set of hypothesis :

`H_0:p=0.45`

`H_a:p\\eq0.45`

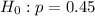
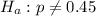
Since the alternative hypothesis
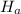`H_a` is two-tailed , so we perform two-tailed test.

Also, it is given that : A random sample of n=76 Americans found 28 with brown eyes.

Sample proportion:
`\hat{p}=(28)/(76)=0.3684`

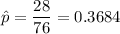
a) The z-statistic would be :-

`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`\Rightarrow\ z=\frac{0.3684-0.45}{\sqrt{(0.45(1-0.45))/(76)}}=-1.4299121397\approx-1.43`

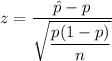
b) P-value for two-tailed test = 2P(Z>|z|)= 2P(z>|-1.43|)

=2P(z>1.43)

=2(1-P(z≤1.43)

=2-2P(z≤1.43)

= 2-2(0.9236)[Using standard z-table]

= 2-1.8472=0.1528

Hence, the P-value of the test= 0.1528