Question

A 1.2-cm-wide diffraction grating has 1000 slits. It is illuminated by light of wavelength 650 nm .What are the angles of the first two diffraction orders?Express your answers using two significant figures separated by a comma.

Answer 1

To solve this problem it is necessary to apply the concepts related to destructive and constructive diffraction formulated in the bragg law.

It is understood by said law that,

`n\lambda = dsin\theta`

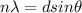
where,

`\lambda = wavelenght`

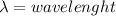
n = Any integer, representing the repetititon of the spectrum.

d = Width

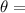`\theta =` It is the angle between the incident rays and the dispersion planes.

PART A) For a diffraction of first order n=1, then

`sin\theta = (1*650*10^(-9))/(((0.012)/(1000)))`

`sin\theta= 0.0541`

`\theta = sin^(-1)(0.0541)`

`\theta = 3.105\°`

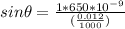
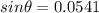
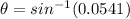
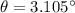
PART B) For a diffraction of second order n=2, then

`sin\theta = (2*650*10^(-9))/(((0.012)/(1000)))`

`sin\theta= 2*0.0541`

`\theta = sin^(-1)(2*0.0541)`

`\theta = 6.21\°`

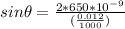
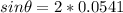
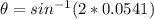
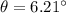
Therefore the angles of the first two diffraction orders are 3.1° and 6.2°