Question

What is the area of trapezoid ABCD?

Enter your answer as a decimal or
whole number in the box. Do not round
at any steps.

Answer 1

First, Identify the Height, Base1 and Base2:

The Height of the trapezoid is AB since it is a right angle that is perpendicular to the base.

Next, the first base can either be AD or BC, I labeled AD as the first and BC as the second. And again the two bases are what the height of the trapezoid is perpendicular to. Hence, AD and BC are the bases.

I will need to use the distance formula to identify the length of the height, and base one and two.

Height= AB

A: (-1,5)

B: (3,2)

`√((x^2-x^1)^2+(y^2-y^1)^2)`

`\sqrt{(3-(-1))^2 +(5-2)^2\\`

`√(4^2+3^2)`

`√(16+9)`

`√(25) = 5`

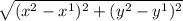
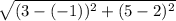
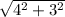
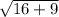
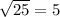
The height of the Trapezoid is 5

Now, I will find base one using the distance formula once more.

Base1= AD

A: (-1,5)

D: (-13, -11)

`√((x^2-x^1)^2+(y^2-y^1)^2)`

`√(((-13)-(-1))^2+((11)-5)^2)`

`√(-12^2+-16^2)`

`√(144+256)`

`√(400)= 20`

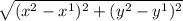
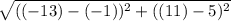
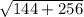
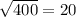
Base one is 20

Onto Base two:

Base2= BC

B: (3,2)

C:(0, -2)

`√((x^2-x^1)^2+(y^2-y^1)^2)`

`√((3-0)^2+((-2)-2)^2)`

`√(3^2+-4^2)`

`√(9+16)`

`√(25 ) = 5`

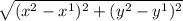
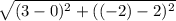
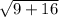
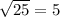
Base two is 5

Finally we can solve for the area of this trapezoid plugging the numbers into the formula.

Area=
`(1)/(2) (base1 +base2) h`

`(1)/(2) (20+5) 5`

`(1)/(2) (25) 5`

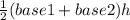
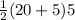
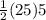
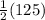`(1)/(2) (125)` = 62.5

The area of the Trapezoid is 62.5

Hint: I used a scientific calculator to solve for the decimal as well as a double check on the square roots.