Answer:
184.08
Explanation:
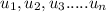 form a sequence exhibiting the following property :
form a sequence exhibiting the following property :
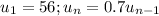
On rewriting,
 ⇒ Ratio of consecutive terms is a constant. Hence, the sequence is a Geometric Progression.
⇒ Ratio of consecutive terms is a constant. Hence, the sequence is a Geometric Progression.
The ratio
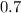 is the common ratio
is the common ratio
 . First term =
. First term =
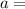
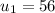 .
.
Sum of
 terms of a Geometric progression is given by
terms of a Geometric progression is given by
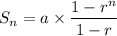 when
when
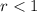 .
.

∴
 to the nearest hundreth is 184.08
to the nearest hundreth is 184.08