Question

The two solids below are similar, and the ratio between the lengths of their edges 4:7 what is the ratio of their surface areas

Answer 1

Answer: 16:9

Explanation:

Answer 2

Answer: 16: 49

Explanation:

If two shapes are similar , then the following condition holds

(i) the ratio of their sides are equal

(ii) If
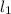`l_(1)` is the length of the first one and
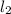`l_(2)` is the length of the second one then:

`(A_(1) )/(A_(2) )` =
`((L_(1) )^(2) )/(L_(2)) ^(2) )`

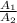Where A stands for the area

(iii)
`(V_(1) )/(V_(2) )` =
`((L_(1) )^(3) )/(L_(2)) ^(3) )`

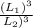
Following theses conditions , the ratio of the lengths of their edges is given to be 4 : 7 , then the ratio of their surface area implies:

`(A_(1) )/(A_(2) )` =
`(4^(2) )/(7^(2) )`

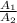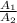`(A_(1) )/(A_(2) )` = 16/49

Therefore the ratio of their surface area is 16: 49