Answer: 1
Explanation:
The formula for calculating the sum of a Geometric series if the common ratio is greater than 1 is given as :
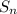 =
=
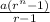
Where
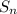 is the sum of terms , a is the first term , r is the common ratio and n is the number of terms.
is the sum of terms , a is the first term , r is the common ratio and n is the number of terms.
From the question:
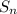 = 3280
= 3280
a = ?
r = 3
n = 8
Substituting this into the formula , we have
3280 =
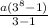
3280 =
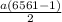
Multiply through by 2 , we have
6560 = a ( 6560)
divide through by 6560, we have
6560/6560 = a(6560)/6560
Therefore : a = 1
The first term of the series is thus 1