By 2035 he will have 2810 fishes.
Solution:
Given, if a farmer stocked his pond with 100 fish in the year 2000 and their population grows at a fixed rate of
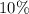 a year
a year
We have to find number of fish he will have in the year 2035. Hint: Use the Rule of 70!
Let the amount of fish in the tank be x. initially x = 100
If x grows
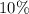 , then you have the original x plus
, then you have the original x plus
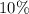 of x.
of x.
Changing from percentage to decimal form (which is almost always necessary and is necessary this time)
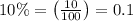 so the growth is
so the growth is
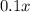 and what was kept was 1x.
and what was kept was 1x.
When you add up what you keep (the original principal) and the interest that you gain you have
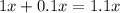
If you do this for two years it is
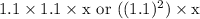 and after n many years you will have
and after n many years you will have

In this problem, n = 35 and x = 100
So, the answer is
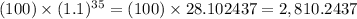 which rounds down to 2,810 fish.
which rounds down to 2,810 fish.