Question

Find the angular speed of any point on one of the

blade of a fan turning at a rate of 800rev/min. find the
Targential speed of the tip of the fan blade if the
distance from its centre to the tip is 150m²​

Answer 1

The angular speed of the blade is, sₐ = 83.78 s⁻¹

The tangential speed of the tip of the fan blade, sₓ = 12567 m/s

Step-by-step explanation:

Given data,

The spinning rate of fan blade, N = 800 rev/min

Converting rpm into radians per sec

`\omega_((rad/s))=( 2 \pi )/(60) * N_(rpm)`

`\omega_((rad/s))=( 2 \pi )/(60) * 800_(rpm)`

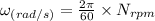
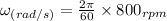
ω = 83.78 s⁻¹

Since speed is only the magnitude of the vector.

The angular speed of the blade is, sₐ = 83.78 s⁻¹

The tangential speed of the tip of the blade at a distance 150 m from its center to the tip is,

v = r ω

Where r is the distance fro the center to the tip

Substituting the values,

v = 150 x 83.78

= 12567 m/s

Hence, the tangential speed of the tip of the fan blade, sₓ = 12567 m/s