Answer:
2.48 m is the length of the rope.
Step-by-step explanation:
Cycle period is 321
Time is 20 second
Wave travels at speeds = 26.4 m/s
We know that,
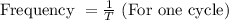
Frequency required for 321 complete cycle in 20 seconds is
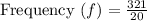
Frequency = 16.05 hz
We know that,
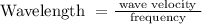
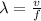
λ = wavelength, the distance between "wave crests" (m)
v = wave velocity, the "speed" that waves are moving in a direction (m/s)
f = frequency, (cycles/ or Hz)
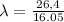
λ = 1.65 m
As per given question "length of the rope has three equal length segment"


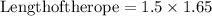
Length of the rope = 2.48 m
Therefore, length of the rope is 2.48 m.