12x +7 < −11 OR 5x −8 > 40

Question

asked Nov 18, 2020 118k views

1 Answer

Jon Onstott · Answer 1 · 2020-11-25T05:54:32+0000

For this case we must resolve each of the inequalities and find the solution set.

Inequality 1:

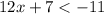
12x + 7 <-11

We subtract 7 from both sides of the inequality:

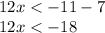
$12x <-11-7\\12x <-18$

We divide between 12 on both sides of the inequality:

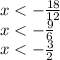
$x <- \frac {18} {12}\\x <- \frac {9} {6}\\x <- \frac {3} {2}$

Thus, the solution is given by all values of x less than
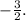
$- \frac {3} {2}.$

Inequality 2:

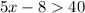
5x-8> 40

We add 8 to both sides of the inequality:

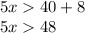
$5x> 40 + 8\\5x> 48$

We divide between 5 on both sides of the inequality:

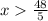
$x> \frac {48} {5}$

Thus, the solution is given by all values of x greater than
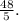
$\frac {48} {5}.$

The solution set is given by:

(-∞,
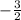$- \frac {3} {2}$ ) U (
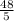$\frac {48} {5}$ ,∞)

Answer:

(-∞,
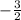$- \frac {3} {2}$ ) U (
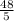$\frac {48} {5}$ ,∞)