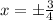Question

What to the 2nd power equal 9/16

Answer 1

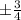`\pm{(3)/(4)}` to the 2nd power equals
`(9)/(16)`

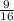
Explanation:

Let the unknown number which is raised to 2nd power be =
`x`

So, the expression can be written as:

`x^2=(9)/(16)`

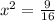
Solving for
`x`

Taking square root both sides to remove the 2nd power.

`√(x^2)=\pm\sqrt{(9)/(16)}`

`x=\pm\sqrt{(9)/(16)}`

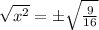
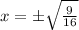
Since 9 and 16 are perfect square, we can write them in 2nd powers of 3 and 4 respectively.

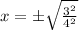
`x=\pm\sqrt{(3^2)/(4^2)}`

∴
`x=\pm{(3)/(4)}`