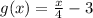Question

Ifg(x) is the inverse of f(x)=4x+12, what is g(x)?

Answer 1

f(x)=1/4x-3

Explanation:

f(x)=4x+12

y=4x+12

--------------

inverse is the opposite

----------------------------------

x=4y+12

4y=x-12

y=(x-12)/4

y=1/4x-12/4

y=1/4x-3

Answer 2

`g(x)=(x)/(4)-3` if g(x) is the inverse of f(x) = 4x+12.

Explanation:

Given that,

f(x) = 4x + 12

To find g(x) Let f(x) = y

y = 4x+12

Subtract 12 from both side

y -12 = 4x + 12 - 12

y – 12 = 4x

Solve to find x

`x=(y)/(4)-(12)/(4)`

`x=(y)/(4)-3`

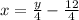
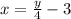
We know that from f(x) = y

`x=f^(-1)(y)`

`f^(-1)(y)=(y)/(4)-3`

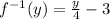
From the question we know that g(x) is the inverse of f(x)

Thus
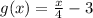`g(x)=(x)/(4)-3` when g(x) is the inverse of f(x)=4x+12.