Answer:
2. f(x) = (x + 3)(x − 1)(x − 4)
Explanation:
As we know that, the standard factored form of an cubic polynomial is:
f(x)= a(x -
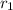 )(x -
)(x -
 )(x -
)(x -
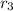 ) where:
) where:
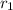 ,
,
 ,
,
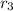 are the roots or x-intercept of the function when it is equal to 0.
are the roots or x-intercept of the function when it is equal to 0.
In this situation, we can see that:
So the the equation of the graph shown is:
f(x) = a(x -
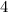 )(x -1)(x +3)
)(x -1)(x +3)
We choose 2, hope it will find you well.