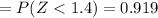Answer:
0.081,0.2621,0.645,0.919
Explanation:
Let X be the average speed of a car driving down freeway
Given that X is normal with mean as 70mph with a standard deviation of 5mph.
To convert to Z score we do

a) the probability that a randomly selected car is driving more than 77mph
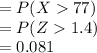
b) probability that a randomly selected car is driving between 65 and 69 mph
=
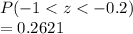
c) the probability that a randonly selected car is driving between 67 and 77mph
=
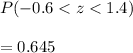
d) the probability that a randomly selected car is driving less than 77mph