Question

1) The mean cost of a steak, broccoli, and ride at the grocery store is $13.04. A sample of 100 restaurants had a mean price of $12.75 and a standard deviation of $2 for the same meal. Run a hypothesis test to determine if it is cheaper to eat at a restaurant than to cook the meal yourself!

Answer 1

Since p >0.05 at 5% significance level we reject that it is cheaper to eat at a restaurant than to cook the meal yourself!

Explanation:

Given that the mean cost of a steak, broccoli, and ride at the grocery store is $13.04.

Sample size n = 100

Sample mean =
`\bar x = 12.75\\s=2`

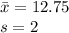
Std error of sample =
`(2)/(√(100) ) =0.20`

`H_0: \bar x = 13.04\\H_a: \bar X <13.04`

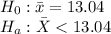
(Left tailed test)

Mean difference =
`13.04-12.75=0.29`

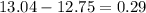
Test statistic = t = mean diff/std error

=
`(0.29)/(0.20) =1.45`

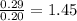
p value one tailed =0.075

Since p >0.05 at 5% significance level we reject that it is cheaper to eat at a restaurant than to cook the meal yourself!