Question

2000 dollars is invested in a bank account at an interest rate of 8 percent per year, compounded continuously. Meanwhile, 11000 dollars is invested in a bank account at an interest rate of 4 percent compounded annually. To the nearest year, When will the two accounts have the same balance? The two accounts will have the same balance after __________________years.

Answer 1

The two accounts will have the same balance after 41.8 years

Step-by-step explanation:

Hi, first, let´s intruduce the mathematical expression for the future value of each investment.

$2,000 compounded continously

`FV=PV*e^(rt)`

`FV=2,000*e^(0.08t)`

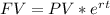
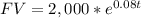
$11,000 at 4% compounded annually (equivalent to effective annual)

`FV=PV(1+r)^(t)`

`FV=11,000(1+0.04)^(t)`

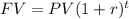
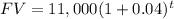
Since the problem is asking when the future value of both investment will reach an equal amount of money, we solve for "t" the resulting expression:

`2,000*e^(0.08t) =11,000(1+0.04)^(t)`

`(e^(0.08t))/((1+0.04)^(t))=(11,000)/(2,000)`

`Ln((e^(0.08t))/((1+0.04)^(t)) ) =Ln((11,000)/(2,000) )`

`Ln(e^(0.08t))-Ln(1.04^(t) ) =Ln((11,000)/(2,000) )`

`0.08*t-t*Ln(1.04) =Ln((11,000)/(2,000) )`

`t(0.08-Ln(1.04) )=Ln((11,000)/(2,000) )`

`t =(Ln((11,000)/(2,000) ))/((0.08-Ln(1.04)) =41.804264=41.8`

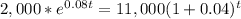
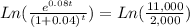
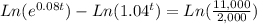
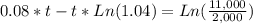
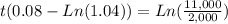
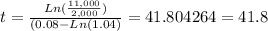
So, this 2 accounts will need 41.8 years to equal their balance. You can check your result by substituting "t" in both equations, they must have the same future value.

`FV=2,000*e^(0.08*41.8)=56,683.79`

`FV=11,000(1+0.04)^(41.8)=56,683.79`

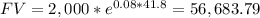
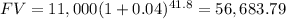
Best of luck.