Answer:
a. There is evidence that the population mean is above $300.
b. There is no evidence that the population mean is above $300.
c. There is no evidence that the population mean is above $300.
d. The director could ask for cheaper similar books.
Explanation:
Let X be the random variable that represents the cost of textbooks. We have observed n = 25 values,
 = 315.4 and s = 43.20. We suppose that X is normally distributed.
= 315.4 and s = 43.20. We suppose that X is normally distributed.
We have the following null and alternative hypothesis
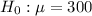 vs
vs
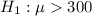 (upper-tail alternative)
(upper-tail alternative)
We will use the test statistic
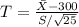 and the observed value is
and the observed value is
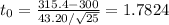 .
.
If
 is true, then T has a t distribution with n-1 = 24 degrees of freedom.
is true, then T has a t distribution with n-1 = 24 degrees of freedom.
a. The rejection region is given by RR = {t | t >
 } where
} where
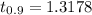 is the 90th quantile of the t distribution with 24 df, so, RR = t . Because the observed value satisty 1.7824 > 1.3178, there is evidence that the population mean is above $300.
is the 90th quantile of the t distribution with 24 df, so, RR = t . Because the observed value satisty 1.7824 > 1.3178, there is evidence that the population mean is above $300.
b. If s = 75, then the observed value is
 . The rejection region for a 0.05 level of significance is RR = {t | t >
. The rejection region for a 0.05 level of significance is RR = {t | t >
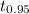 } where
} where
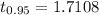 is the 95th quantile of the t distribution with 24 df, so, RR = t . Because the observed value does not fall inside the rejection region, there is no evidence that the population mean is above $300.
is the 95th quantile of the t distribution with 24 df, so, RR = t . Because the observed value does not fall inside the rejection region, there is no evidence that the population mean is above $300.
c. If
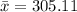 and s = 43.20, the observed value is
and s = 43.20, the observed value is
 . For RR = t we have that the observed value does not fall inside RR, therefore, there is no evidence that the population mean is above $300.
. For RR = t we have that the observed value does not fall inside RR, therefore, there is no evidence that the population mean is above $300.
d. Because the director of admissions is concerned about the high cost of textbooks, and there is evidence that the population mean of costs is above $300, the director could ask for cheaper similar books.