Step-by-step explanation:
The given data is as follows.
Q = 2 kW,
 = 775 K
= 775 K
 = 300 K
= 300 K
The relation between entropy and heat energy is as follows.
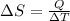
Therefore, calculate the entropy at each temperature as follows.
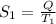
=
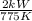
=
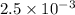 kW/K
kW/K
Also,
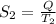
=

=
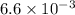 kW/K
kW/K
Hence, the change in entropy will be calculated as follows.
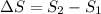
=
 kW/K
kW/K
=
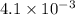 kW/K
kW/K
or, = 0.0041 kW/K
Thus, we can conclude that the rate at which the entropy of the two reservoirs changes is 0.0041 kW/K.