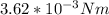To solve this problem it is necessary to take into account the concepts related to the magnetic moment and the torque applied over magnetic moments.
For the case of the magnetic moment of a loop we have to,

Where
I = Current
A = Area of the loop
Moreover the torque exerted by the magnetic field is defined as,
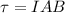
Where,
I = Current
A = Area of the loop
B = Magnetic Field
PART A) First we need to find the perimeter, then
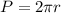
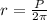
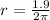

The total Area of the loop would be given as,
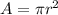
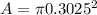
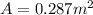
Substituting at the equation of magnetic moment we have
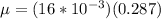
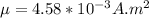
Therefore the magnetic moment of the loop is

PART B) Replacing our values at the equation of torque we have that
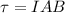
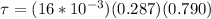

Therefore the torque exerted by the magnetic field is