Answer:
The energy stored in the later case is equal to the energy stored in the former case of the spring.
Step-by-step explanation:
For a spring we have the expression of kinetic energy as:

where:
k= elastic constant of the spring
x= length of deflection of the spring from the mean position
Here we are given two cases:
CASE:1
x=d
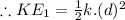
CASE:2
x=-d
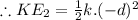
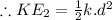
So, we get
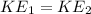
Just the difference in the two cases is that there is deflection of the spring in the opposite direction.