Question

You want to build a wheelchair ramp leading up to your house. Your front door is 2 feet higher than the driveway and you would like the grade of the ramp to be 7%. (a) What is the angle, θ, that the ramp forms with the driveway? (Round your answer to three decimal places.) s ° (b) How long does the driveway have to be to build this ramp? (Round your answer to two decimal places.) s ft (c) How long will the ramp be? (Round your answer to two decimal places.)

Answer 1

Answer: (a) The angle the ramp forms with the driveway, s° = 4.004° (3 d.p)

(b) The driveway has to be, s = 28.57 ft

(c) The ramp will be 28.64 ft long

Explanation:

First key thing to know is that the %grade of a ramp = rise/ramp run

%grade of a ramp = 7% = 0.07

(Kindly find attached a diagram to assist with understanding).

Also note that, the ramp run is not the same as the ramp length

(a) the angle, θ, is the angle of slope between the driveway and the ramp,

tan θ = 0.07,

θ = tan⁻¹ 0.07 = 4.004° (3 d.p)

(b) the length of the driveway (s) is the same as the length of the ramp run, so, %grade of a ramp = rise/ramp run

0.07 = 2/s

s = 2/0.07 = 28.57 ft (2 d.p)

(c) the length of the ramp can be found by using Pythagoras' theorem,

L = ramp length =
`\sqrt{rise^(2) + ramprun^(2) }`

L =
`\sqrt{2^(2) +28.571^(2) }`

L =
`√(820.3041)`

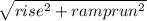
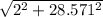
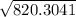
L = 28.64 ft (2 d.p)