Question

(10%) Problem 10: A 7.25-kg bowling ball moving at 9.85 m/s collides with a 0.875-kg bowling pin, which is scattered at an angle of θ = 21.5° from the initial direction of the bowling ball, with a speed of 10.5 m/s.

Answer 1

given,

mass of bowling ball = 7.25 Kg

moving speed of the bowling ball = 9.85 m/s

mass of bowling in = 0.875 Kg

scattered at an angle = θ = 21.5°

speed after the collision = 10.5 m/s

angle of the bowling ball

`tan \theta_1 = (-[m_2v_2Sin \theta_2])/(m_1v_1 - (m_2v_2cos \theta_2))`

`tan \theta_1 = (-[0.875* 10.5 * Sin 21.5^0])/(7.25* 9.85 - (0.875* 10.5 * cos 21.5^0))`

`tan \theta_1 = (-[3.3672])/(62.86)`

`tan \theta_1 = 0.0536`

`\theta_1 =-3.066^0`

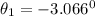
b) magnitude of final velocity

`v = (-m_2v_2sin\theta_2)/(m_1 sin\theta_1)`

`v = (-0.875 * 10.5 sin21.5^0)/(7.25 sin(-3.066^0))`

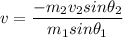
v = 8.68 m/s