Question

The amount of time single men and women spend on house work is measured for 15 single women and 25 single men.

For the women the mean was 7 hours/week with a standard deviation of 1.5. For the men the mean was 4.5 hours/week with a standard deviation of 1.1.

What is the value of the pooled standard deviation for the difference in mean time spent on housework between single men and women?
A. 1.30
B. 0.45
C. 1.59
D. 1.26

Answer 1

Answer: Option 'D' is correct.

Explanation:

Since we have given that

Number of single women = n₁ = 15

Number of single men = n₂ = 25

Mean for men = 7 hours per week

Mean for women = 4.5 hours per week

Standard deviation for men = s₁=1.5

Standard deviation for women = s₂=1.1

We need to find the value of the pooled standard deviation for the difference in mean time spent on housework single men and women.

So, Value of pooled variance is given by

`((n_1-1)s_1^2+ (n_2-1)s_2^2)/(n_1+n_2-2)\\\\=((15-1)(1.5)^2+(25-1)(1.1)^2)/(15+25-2)\\\\=(14* 2.25+24* 1.21)/(38)\\\\=(60.54)/(38)\\\\=1.59`

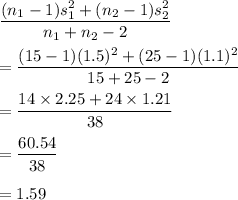
So, Value of pooled standard deviation is given by

`√(Variance)=√(1.59)=1.26`

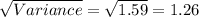
Hence, Option 'D' is correct.