Answer:
The area of the smaller triangle is 75.
Explanation:
Here, the ratio of the sides of the similar triangle are 5 : 6
The area if the larger triangle = 108
let us assume that the area of the smaller triangle = m
By the Theorem:
In two similar triangles, the ratio of the areas of similar triangles is the square of the ratio of their sides.
Similarly, here
/(6)) ^2](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hcpjbcnyq46lpi9i1p08lv8a8mm74dbanj.png) = \frac{m}{108}[/tex]
= \frac{m}{108}[/tex]
⇒
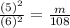
or,

⇒ m = 75
Hence, the area of the smaller triangle is 75.