Question

Sofia can type the work in 10 hours. Nova can do it in 15 hours. They work together for 4 hours, then Sofia and Nova finish the job. How long did it take to do the entire job?

Answer 1

Sofia and Nova together completes the work in 6 hours.

SOLUTION:

Given, Sofia can type the work in 10 hours.

Nova can do it in 15 hours.

They work together for 4 hours, then Sofia and Nova finish the job.

We have to find time taken to do the entire job

Now, work done by Sofia in 1 hour
`=(1)/(10)`

And work done by Nova in 1 hour
`=(1)/(15)`

Then, when they are together, work done in 1 hour
`=(1)/(10)+(1)/(15)=(1)/(5)\left((1)/(2)+(1)/(3)\right)=(1)/(5)\left((3+2)/(6)\right)=(1)/(5) * (5)/(6)=(1)/(6)`

So,
`\text { total required time }=(1)/((1)/(6))=6 \text { hours }`

Answer 2

2 days.

Explanation:

Let, Sofia can type the x amount of work in 10 hours.

So, in one hour Sofia can type
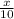`(x)/(10)` amount of work.

Again, Nova can type x amount of work in 15 hours.

So, in one hour Nova can type
`(x)/(15)` amount of work.

Hence, if they work together, they can type
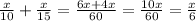`(x)/(10) + (x)/(15) = (6x + 4x)/(60) = (10x)/(60) = (x)/(6)` amount of work in one hour.

Therefore, working together they can type the x amount of work in
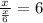`(x)/((x)/(6) ) = 6` days.

So, they have to work for (6 - 4) = 2 days more to finish the work. (Answer)