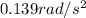Question

A mass attached to a 50.0 cm long string starts from rest and is rotated 40 times in one minute before reaching a final angular speed. Determine the angular acceleration of the mass, assuming that it is constant.

Answer 1

To solve this problem it is only necessary to apply the kinematic equations of angular motion description, for this purpose we know by definition that,

`\theta = (1)/(2)\alpha t^2 +\omega_0 t + \theta_0`

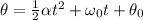
Where,

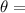`\theta =` Angular Displacement

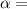`\alpha =`Angular Acceleration

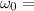`\omega_0 =` Angular velocity

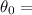`\theta_0 =`Initial angular displacement

For this case we have neither angular velocity nor initial angular displacement, then

`\theta = (1)/(2)\alpha t^2`

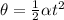
Re-arrange for
`\alpha,`

`\alpha = (2\theta)/(t^2)`

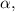
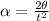
Replacing our values,

`\alpha = (2(40rev*(2\pi rad)/(1rev)))/(60^2)`

`\alpha = 0.139rad/s`

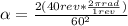
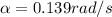
Therefore the ANgular acceleration of the mass is
`0.139rad/s^2`