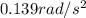To solve this problem it is only necessary to apply the kinematic equations of angular motion description, for this purpose we know by definition that,
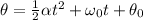
Where,
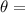 Angular Displacement
Angular Displacement
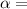 Angular Acceleration
Angular Acceleration
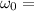 Angular velocity
Angular velocity
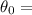 Initial angular displacement
Initial angular displacement
For this case we have neither angular velocity nor initial angular displacement, then
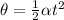
Re-arrange for
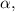
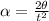
Replacing our values,
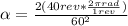

Therefore the ANgular acceleration of the mass is