Answer:
38.847 seconds
Step-by-step explanation:
m = Mass
x = Compression of spring
k = Spring Constant
g = Acceleration due to gravity = 9.81 m/s²
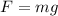
From Hooke's law
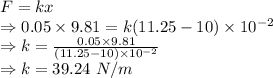
Additional mass
m = 0.1+0.05 = 0.15 kg
Angular frequency
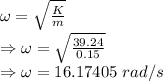
Time for one oscillation is given by
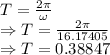
For 100 oscillations

The time needed for hundred oscillations is 38.847 seconds