Answer:
0.4,08,>15000, No
Explanation:
Given that we are interested in bidding on a piece of land and we know one other bidder is interested. The seller announced that the highest bid in excess of $10,000 will be accepted.
Competitor Bid is U (10000,15000)
If your bid is more than competitors bid your bid will be accepted
a) Suppose you bid $12,000. What is the probability that your bid will be accepted
=
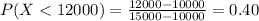
b) Suppose you bid $14,000. What is the probability that your bid will be accepted
=
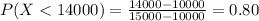
c) amount should you bid to maximize the probability that you get the
property>15000 because the prob to get the bid is
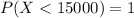
d) Suppose you know someone who is willing to pay you $16,000 for the property. Would you consider bidding less than the amount in part (c)? Why or why not
No. Bid for 15000 will allow to win the bid and also get a profit of 1000 dollars by selling immediately.