Answer:
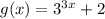
The transformation that occurs from
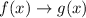 is compression by 3 units horizontally and shift of 4 units upwards.
is compression by 3 units horizontally and shift of 4 units upwards.
Explanation:
Given
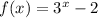

Translation Rules:
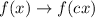
If
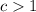 the function is compressed
the function is compressed
 units horizontally.
units horizontally.
If
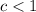 and
and
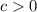 the function stretches
the function stretches
 units horizontally.
units horizontally.
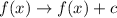
If
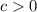 the function shifts
the function shifts
 units to the up.
units to the up.
If
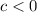 the function shifts
the function shifts
 units to the down.
units to the down.
Applying the rules to

Step 1
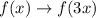
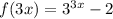
[compressed
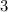 units horizontally]
units horizontally]
Step 2
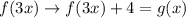
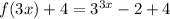
∴
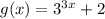
[shifts 4 nits up]
∴ The transformation that occurs from
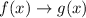 is compression by 3 units horizontally and shift of 4 units upwards.
is compression by 3 units horizontally and shift of 4 units upwards.