Question

You have two synchronously vibrating objects in an infinitely large pool. The distance between them is 6.0 m. Their frequency of vibration is 2.0 Hz and the wave speed is 4.0 m/s. The vibrations are sinusoidal. Neglect the decrease of amplitude with distance.

A. Find a minimum distance from one of the objects to a location between objects where the water does not vibrate. Note that the required location should not coincide with the location of the chosen object.
B.Find a minimum distance from one of the objects to a location between objects where the water vibrates with the largest amplitude. Note that the required location should not coincide with the location of the chosen object.

Answer 1

To solve the problem it is necessary to apply the concepts related to wavelength.

By definition we know that the wavelength is expressed as

`\lambda = (v)/(f)`

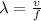
Where,

v= velocity

f = frequenciy

On the other hand we have that the distance when there is vibration can be calculated as

`\Delta x = n\lambda`

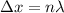
Where n is an integer for standing wave pattern, or harmonic, number.

Part A ) The distance between the two objects is basically

`\Delta x = 6-x`

`\Delta x = 6.2x`

The velocity is

`v=f\lambda`

`\lambda = (v)/(f)`

`\lambda = (4m/s)/(2Hz)`

`\lambda =2m`

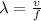
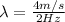
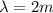
On the one hand the the distance for the no vibration is

`\Delta x = (n+(1)/(2))\lambda`

`\Delta x = (0+(1)/(2))\lambda`

`\Delta x = (\lambda)/(2)`

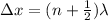
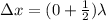
Replacing the value for x,

`6-2x =(2m)/(2)`

`6-2x=1`

`x=2.5m`

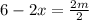
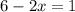
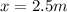
On the other hand the minimum distance is:

`\Delta x = (n+(1)/(2))\lambda`

`6-2x=\frac{n+(1)/(2)}\lambda`

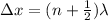
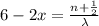
Re-arrange to x

`x=2.5-n`

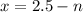
For positive x, the value of n is
`n_(max)=2`

`x = 2.5-2`

`x=0.5m`

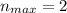
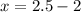
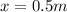
Therefore the required distance is 0.5m

PART B) The maximum vibration, the distance is

`\Delta x= n\lambda`

`6-2x = n(2)`

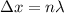
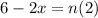
For the minimum distance, n is maximum, therefore

`6-2x=2*2`

`x=1m`

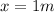
Therefore the required minimum distance is 1m.