2 Answers

Hbit · Answer 1 · 2020-09-24T01:48:40+0000

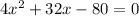4 x^(2)+32 x-80=0 is the required equation to calculate width of rectangular frame that has a total area of 140 square inches.

Given that,

Length of a rectangular frame is given as 2x + 10

Width of the rectangular frame is given as 2x + 6

Total area = 140 square inches

The area of rectangular frame is given as:

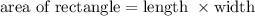
$\text {area of rectangle}=\text {length } * \text {width}$

Plugging in values, we get

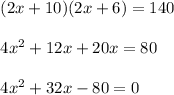
$\begin{array}{l}{(2 x+10)(2 x+6)=140} \\\\ {4 x^(2)+12 x+20 x=80} \\\\ {4 x^(2)+32 x-80=0}\end{array}$

This is the required equation to calculate width of rectangular frame

Solve the above quadratic equation to get the value of "x"

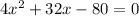
4 x^(2)+32 x-80=0

Use the quadratic equation formula:

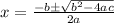
$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}$

Here a = 4 ; b = 32 ; c = -80

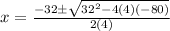
$x=\frac{-32 \pm \sqrt{32^(2)-4(4)(-80)}}{2(4)}$

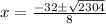
$x=(-32 \pm √(2304))/(8)$

x = 2 or x = -10

Now measurement cannot be negative, so taking the positve value of "x", we can calculate the width

So put "x" = 2

Width of the rectangular frame = 2x + 6 = 2(2) + 6 = 10

Thus the width of frame is 10 inches

Please log in or register to add a comment.