Question

A $1 bet in a state lottery Pick 3 game pays $500 if the 3-digit number you choose exactly matches the winning number, which is drawn at random. Here's the distribution of the payoff X:

Payoff X $0 $500

Probability 0.999 0.001


Each day's drawing is independent of other drawings.


a) What's the mean and the standard deviation of X?

b)Joe buys a Pick 3 ticket twice a week. What does the law of large numbers say about the average payoff Joe receives from his bets?

c) What does the central limit theorem say about the distribution of Joe's average payoff after 104 bets in a year?

Answer 1

Explanation:

Given that in a $1 bet in a state lottery Pick 3 game pays $500 if the 3-digit number you choose exactly matches the winning number, which is drawn at random. Here's the distribution of the payoff X:

we find that each game is independent of the other and probability for success in each game p = 0.001 is constant

X is binomial

a) Mean of X = E(X) =
`np = 0.001 n` where n is no of tickets

Var of (X) = npq = 0.001 np

Std dev (X) =
`√(0.001*0.999n) \\=0.0317√(n)`

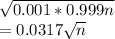
b) Here n =3 per week

when he purchases more tickets such n tends to infinity sample mean would almost equal to the population mean.

i.e. he can expect 0.001 per trial only.

c) Central limit theorem says for 104 bets the pay off would be approxy normal with mean = 0.104 and std dev = 0.322