Question

A Ferris Wheel is built such that the height in feet above ground of a seat on the wheel at time t seconds can be modeled by h(t) = 53 + 50sin((pi/16)t - (pi/2)) The wheel makes one revolution every 32 seconds. The ride begins when t = 0. During the first 32 seconds of the ride, when will a person on the Ferris Wheel be 53 feet above the ground?

Answer 1

Answer:it’s 101 feet

Explanation:

Ap3x Approved

Answer 2

at time, t = 8 seconds and t = 24 seconds Ferris Wheel be 53 feet above the ground

Explanation:

Data provided in the question:

height in feet above ground of a seat on the wheel at time t seconds is

modeled as

h(t) =
`53 + 50\sin(((\pi t)/(16) - (\pi)/(2))`

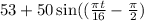
now,

at height 53 above the ground, we get the equation as:

53 =
`53 + 50\sin((\pi t)/(16) - (\pi)/(2))`

or

`50\sin((\pi t)/(16) - (\pi)/(2))` = 53 - 53

or

`\sin((\pi t)/(16) - (\pi)/(2))` = 0

also,

sin(0) = 0

and,

sin(π) = 0

therefore,

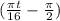`((\pi t)/(16) - (\pi)/(2))` = 0

or

`(\pi t)/(16) = (\pi)/(2)`

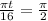
or

t = 8 seconds

and,

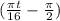`((\pi t)/(16) - (\pi)/(2))` = π

or

`(\pi t)/(16)= \pi + (\pi)/(2)`

or

`(\pi t)/(16)= (3\pi)/(2)`

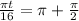
or

t = 24 seconds

Hence,

the at time, t = 8 seconds and t = 24 seconds Ferris Wheel be 53 feet above the ground