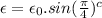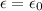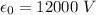Answer:
Step-by-step explanation:
Given:
no. of turns in the coil,
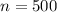
area of the coil,

average emf induced,

angle turned by the coil,
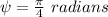
time taken to sweep the given angle,
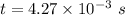
peak emf,
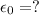
We have the relation between peak emf and average emf as:
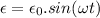 .............................(1)
.............................(1)
where:

we already know the value:
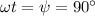
From eq. (1) we have: