Question

A 39.0-kg child swings in a swing supported by two chains, each 2.98 m long. The tension in each chain at the lowest point is 416 N. (a) Find the child's speed at the lowest point. m/s (b) Find the force exerted by the seat on the child at the lowest point. (Ignore the mass of the seat.) N (upward)

Answer 1

a)v=5.81 m/s

b)N= 831.77 N

Step-by-step explanation:

Given that

m = 39 kg

r= 2.98 m

T= 416 N

a)

Lets take speed of the boy at the lowest position is v m/s

The radial force Fc

`F_c=(mv^2)/(r)`

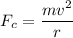
The tension in the chain is T

`2T-mg=(mv^2)/(r)`

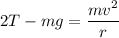
Now by putting the values

`2T-mg=(mv^2)/(r)`

`2* 416-39* 10=(39* v^2)/(2.98)`

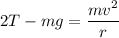
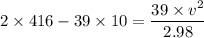
v²=33.77

v=5.81 m/s

b)

Lets take normal force = N

`N-mg=(mv^2)/(r)`

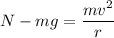
Now by putting the values

`N-mg=(mv^2)/(r)`

`N=mg +(mv^2)/(r)`

`N=39* 10+(39* 5.81^2)/(2.98)`

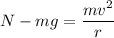
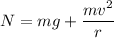
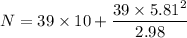
N= 831.77 N