Question

Suppose that a monopolist faces linear demand given by Q(p)-100-2*p The monopolist also pays a marginal cost of $1 for each unit produced. What is the price that the monopolist will set to maximize its profits? A. 25.5 B. 51 C. 50.5 D. 24.5

Answer 1

A. 25.5

Step-by-step explanation:

The monopolist's profit function is:

Profit = Price*Q(Price) - marginal cost

Since the marginal cost is $1 for each unit produced, profit is given by:

Profit = Price*Q(Price) - 1*Q(Price)

Since the Q(p) function is given, profits are given by:

`Profit= p*(100-2*p) - (100-2*p)\\Profit = -2p^2 +102p - 100`

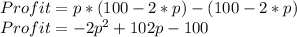
The maximum value for the profit function occurs at the point in which the function's derivative equals zero, therefore:

`(d(Profit))/(dp)=(d(-2p^2 +102p - 100 ))/(dp)\\(d(Profit))/(dp)= -4p +102 = 0\\p=(102)/(4) \\p=25.5`

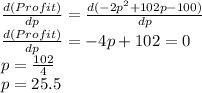
The price that the monopolist will set to maximize its profits is 25.5.