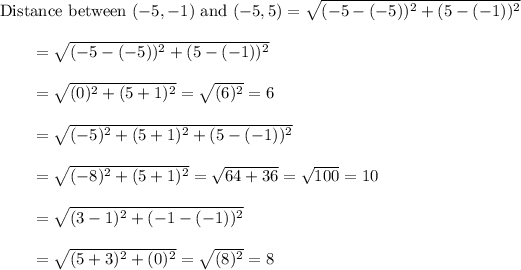The side lengths of triangle are 6 units, 8 units and 10 units.
SOLUTION:
Given that, we have to find what is the length side of a triangle that has vertices at (-5, -1), (-5, 5), and (3, -1)
We know that, distance between two points
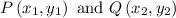 is given by
is given by
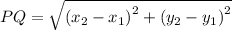
Now,