Answer: 6,8 and 10
Explanation:
To find the length , all we need to find is the distance between each point ,
the formula for calculating distance between two points is given by :
D =
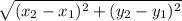
Let the points be :
A ( -5,-1)
B(-5,5)
C(3,-1)
Calculating the length AB , we have
D1 =
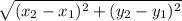
D1 =
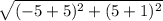
D1 =
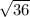
D1= 6
Calculating the length AC , we have
D2 =
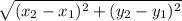
D2 =
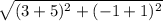
D2 =
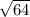
D2 = 8
Calculating the length BC , we have
D3 =
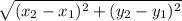
D3 =

D3 =
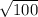
D3 = 10
Therefore ,the length of the sides of the triangle are 6,8 and 10