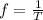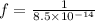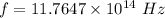Answer:
(a)

(b)
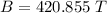
(c)
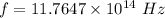
(d)
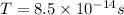
Step-by-step explanation:
Given:
Kinetic Energy of an electron,
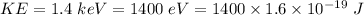
radius of the orbit,
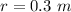
we have:
mass of an electron,
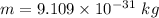
charge on an electron,
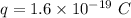
(a)
we know:
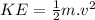
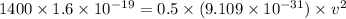

(b)
We also have the relation after the comparison of forces(centripetal and magnetic) on a moving charge in a magnetic field as:
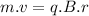 ...........................(1)
...........................(1)
where:
B = magnetic field normal to the plane of circulating charge
putting respective values in eq. (1)
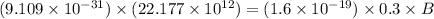
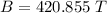
(d)
angular speed:
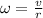
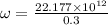
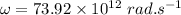
∴Time taken for 1 radian:
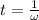
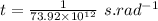
Now time take for 1 circulation i.e. 2π radians(Time period):
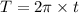
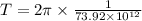
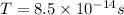
(c)
we know frequency :