Question

When the current in a toroidal solenoid is changing at a rate of 0050 N5, the magnitude of the induced emf is 126 mV,When tire current equals 1.40 A, the average flux through each turn of the solenoid is 000285 Wb. How many turns doesthe solenoid have?

Answer 1

N = 1238

Step-by-step explanation:

It is given that,

Change in current in the toroidal solenoid,
`(dI)/(dt)=0.05\ A/s`

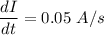
Induced emf in the solenoid,
`\epsilon=126\ mV=126* 10^(-3)\ V`

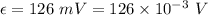
Current in tire, I = 1.4 A

Flux in the solenoid,
`\phi=0.00285\ Wb`

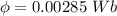
The induced emf in the solenoid is given by :

`\epsilon=L(dI)/(dt)`

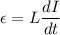
L is the self inductance of the solenoid

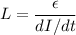`L=(\epsilon)/(dI/dt)`.........(1)

The self inductance of solenoid is given by :

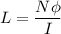`L=(N\phi)/(I)`............(2)

From equation (1) and (2) :

`(N\phi)/(I)=(\epsilon)/(dI/dt)`

`N=(\epsilon I)/(\phi (dI/dt))`

`N=(126* 10^(-3)* 1.4)/(0.00285* 0.05)`

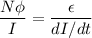
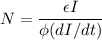
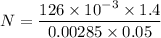
N = 1237.89

or

N = 1238

So, the number of turns in the solenoid is 1238. Hence, this is the required solution.