Answer:
 and
and
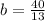
Explanation:
The equation of curve is
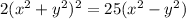
We need to find the equation of the tangent line to the curve at the point (-3, 1).
Differentiate with respect to x.
![2[2(x^2+y^2)(d)/(dx)(x^2+y^2)]=25(2x-2y(dy)/(dx))](https://img.qammunity.org/2020/formulas/mathematics/high-school/gg4zkv04qwfh0akmm72dgrzg79g8p4nyfq.png)
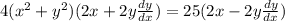
The point of tangency is (-3,1). It means the slope of tangent is
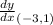 .
.
Substitute x=-3 and y=1 in the above equation.
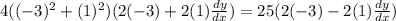
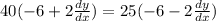

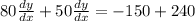
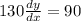
Divide both sides by 130.
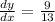
If a line passes through a points
 with slope m, then the point slope form of the line is
with slope m, then the point slope form of the line is

The slope of tangent line is
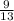 and it passes through the point (-3,1). So, the equation of tangent is
and it passes through the point (-3,1). So, the equation of tangent is
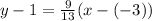
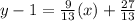
Add 1 on both sides.
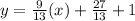
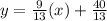
Therefore,
 and
and
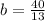 .
.