Question

A 25 kg block is held against a compressed spring and then the spring is allowed to decompress giving the block a velocity. The block then slides to the right on a horizontal frictionless surface and then up a frictionless incline.

Find the maximum height that the block reaches if the incline is 19.5 ∘ . All surfaces are frictionless, the spring constant is 1300 N/m and the initial spring compression is 26.4cm.

Answer 1

h=18.05 cm

Step-by-step explanation:

Given that

m= 25 kg

K= 1300 N/m

x=26.4 cm

θ= 19.5 ∘

When the block just leave the spring then the speed of block = v m/s

From energy conservation

`(1)/(2)Kx^2=(1)/(2)mv^2`

`Kx^2=mv^2`

`v=\sqrt{(kx^2)/(m)}`

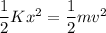
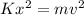
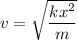
By putting the values

`v=\sqrt{(kx^2)/(m)}`

`v=\sqrt{(1300* 0.264^2)/(25)}`

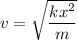
v=1.9 m/s

When block reach at the maximum height(h) position then the final speed of the block will be zero.

We know that

`V_f^2=V_i^2-2gh`

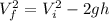
By putting the values

`0^2=1.9^2-2* 10* h`

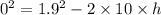
h=0.1805 m

h=18.05 cm